Summary
A while back Twitter once again lost its collective mind and decided to rehash the logistic regression versus linear probability model debate for the umpteenth time. The genesis for this new round of chaos was Gomila (2019), a pre-print by Robin Gomila, a grad student in psychology at Princeton.
So I decided to learn some more about the linear probability model (LPM), which has been on my todo list since Michael Weylandt suggested it as an example for a paper I’m working on. In this post I’ll introduce the LPM, and then spend a bunch of time discussing when OLS is a consistent estimator.
Update: I turned this blog post into somewhat flippant, meme-heavy slides.
What is the linear probability model?
Suppose we have outcomes
Essentially we clip
At points throughout this post we will also be interested in Gaussian GLMs. In slightly different notation, we can write all of these models as follows:
The OLS estimator
When people refer to the linear probability model, they are referring to using the Ordinary Least Squares estimator as an estimator for
Most people have seen the OLS estimator derived as the MLE of a Gaussian linear model. Here we have binary data, which is definitely non-Gaussian, and this is aesthetically somewhat unappealing. The big question is whether or not using
A bare minimum for inference
When we do inference, we pretty much always want two things to happen. Given our model (the assumptions we are willing to make about the data generating process):
- our estimand should be identified, and
- our estimator should be consistent.
Identification means that each possible value of the estimand should correspond to a distinct distribution in our probability model. When we say that we want a consistent estimator, we mean that our estimator should recover the estimand exactly with infinite data. All the estimands in the LPM debate are identified (to my knowledge), so this isn’t the big deal here. But consistency matters a lot!
Gomila (2019) claims that
And this is the point that I got pretty confused, because the big question is: consistent under what model? Depending on who you ask, we could conceivably be assuming that the data comes from:
- a Gaussian GLM (linear regression),
- the linear probability model, or
- a binomial GLM (logistic regression).
Consistency of the OLS estimator
The easiest case is when we assume that a Gaussian GLM (linear regression model) holds. In this case,
When the linear probability model holds,
At this point the main result of Horrace and Oaxaca (2003) becomes germane. It goes like this: the OLS estimator is consistent and unbiased under the linear probability model if
Unless the range of
is severely restricted, the linear probability model cannot be a good description of the population response probability .
Here are some simulations demonstrating this bias and inconsistency when the
We discussed this over Twitter DM, and Gomila has since updated the code, but I believe the new simulations still do not seriously violate the DeclareDesign particularly well so I gave up. Many kudos to Gomila for posting his code for public review.
Anyway, the gist is that OLS is consistent under the linear probability model if
What if logistic regression is the true model?
Another reasonable question is: what happens to
The intuition behind this comes from M-estimation1, which we digress into momentarily. The idea is to observe that
which has a global minimizer
should be zero at
In particular, M-estimation theory tells us that
We can use this to derive a sufficient condition for consistency; namely OLS is consistent for
So a sufficient condition for the consistency of OLS is that
That is, if the expectation is linear in some model parameter
where we take
The sufficient condition is also a necessary condition, and if it is violated
Returning from our digression into M-estimation, we note the condition that
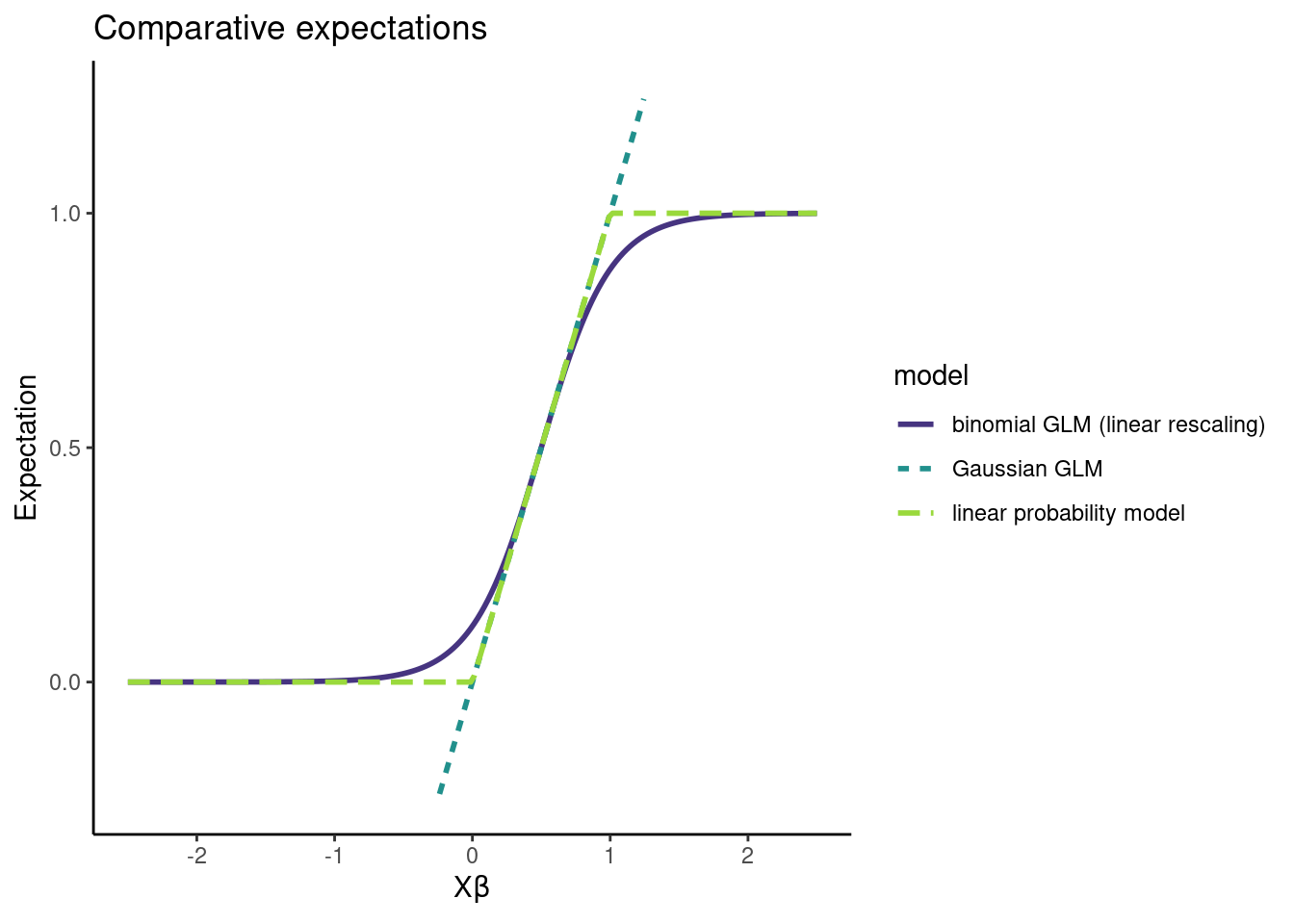
Anyway, the expectation of a binomial GLM is
Looking at the expectations of the models, we can see they aren’t wildly different:
Note that, under the LPM,
So maybe don’t toss the LPM estimator out with the bath water. Sure, the thing is generally inconsistent and aesthetically offensive, but whatever, it works on occasion, and sometimes there will be other practical considerations that make this tradeoff reasonable.
Where the estimator comes from doesn’t matter
Bayes Twitter in particular had a number of fairly vocal LPM opponents, on the basis that
This might seem like a dealbreaker, but it doesn’t bother me. Where the estimator comes from doesn’t actually matter. If it has nice properties given the assumptions you are willing to make, you should use it! Estimators derived under unrealistic models4 often turn out to be good!
In a bit more detail, here’s how I think of model checking:
- There’s an estimand I want to know
- I make some assumptions about my data generating process
- I pick an estimator that has nice properties given this data generating process
The issue here is that my assumptions about the data generating process can be wrong. And if my modeling assumptions are wrong, then my estimator might not have the nice properties I want it to have, and this is bad.
The concern is that using
That’s not really what’s going on though. Instead, we start by deriving an estimator under the linear regression model. Then, we show this estimator has nice properties under a new, different model. To do model checking, we need to test whether the new, different model holds. Whether or not the data comes from a linear regression is immaterial.
Nobody who likes using
What about uncertainty in our estimator?
So far we have established that
In practice, we also care about the uncertainty in
It only took several weeks of misreading Boos and Stefanski (2013) and asking dumb questions on Twitter to figure this out. Thanks to Achim Zeileis, James E. Pustejovsky, Cyrus Samii for answering those questions. Note that White (1980) is another canonical paper on robust standard errors, but it doesn’t click for me like the M-estimation framework does.
Takeaways
This post exists because I wasn’t sure when
Properties of estimators are always with respect to models, and it’s hard to discuss which estimator is best if you don’t clarify modeling assumptions.
If there are multiple reasonable estimators, fit them all. If they result in substantively different conclusions: congratulations! Your data is trash and you can move on to a new project!
If you really care about getting efficient, consistent estimates under weak assumptions, you should be doing TMLE or Double ML or burning your CPU to a crisp with BART5.
Anyway, this concludes the “I taught myself about the linear probability model and hope to never mention it again” period of my life. I look forward to my mentions being a trash fire.
References
Footnotes
An M-estimator
for some function
then
and
exist for all
so life is pretty great and we can get asymptotic estimates of uncertainty for
In a lot of experimental settings that compare categorical treatments, you fit a fully saturated model that allocates a full parameter to the mean of each combination of treatments.
Let’s prove this for logistic regression first. Suppose we have groups
where
Put
Thus
Okay, now we’re halfway done but we still need to show consistency under the LPM. We assume the model is
Putting
Thus
Michael Weylandt suggested the following example as an illustration of this. Suppose we are going to compare just two groups, so
We know that
This is a concrete application of the result in the previous footnote:
I.I.D. assumptions are often violated in real life, for example!
My advisor made an interesting point about critiquing assumptions the other day. He said that it isn’t enough to say “I don’t think that assumption holds” when evaluating a model or an estimator. Instead, to show than the assumption is unacceptable, he claims you need to demonstrate that making a particular assumption results in some form of undesirable inference.↩︎
Gomila also makes an argument against using